同济大学出版社高等数学的思维导图_思维导图模板_知犀官网

同济大学出版社高等数学的思维导图

作者：彭權

0浏览2023-05-10 17:44:36

下载

使用模板已被用12次

# 同济大学高等数学知识体系

## 高等数学上册

- 第一章函数与极限

- 一、函数的概念与性质

- 二、初等函数

- 三、极限的概念与性质

- 四、极限的计算方法

- 五、单侧极限及其应用

- 六、无穷小与无穷大

- 七、极限存在准则及夹逼定理

- 八、函数的连续性及其应用

- 第二章导数与微分

- 一、导数的概念与几何意义

- 二、导数的计算法则

- 三、高阶导数与莱布尼茨公式

- 四、隐函数求导法

- 五、相关变化率与线性近似

- 六、微分的概念与计算

- 七、微分中值定理及其应用

- 第三章微分中值定理与导数的应用

- 一、罗尔定理及其应用

- 二、拉格朗日中值定理及其应用

- 三、柯西中值定理及其应用

- 四、利用导数研究函数的单调性和曲线形状

- 五、函数的凸性和拐点

- 六、最值问题

- 第四章不定积分

- 一、不定积分的概念与性质

- 二、基本积分公式

- 三、换元积分法

- 四、分部积分法

- 五、有理函数的积分

- 六、三角函数的积分

- 七、反三角函数的积分

- 八、简单的变量代换

- 第五章定积分

- 一、定积分的概念及其几何意义

- 二、定积分的计算

- 三、定积分的性质

- 四、变限积分与微积分学基本定理

- 五、无穷小量与无穷大量

- 六、广义积分

- 第六章微积分基本定理的应用

- 一、牛顿－莱布尼茨公式

- 二、平均值定理及其应用

- 三、函数的连续性、可导性与积分中值定理

- 四、洛必达法则及其应用

- 五、泰勒公式及其应用

- 六、不等式及极值问题

## 高等数学下册

- 第七章多元函数微分学

- 一、多元函数的概念

- 二、偏导数及其计算法则

- 三、全微分与全微分公式

- 四、复合函数求导法及隐函数定理

- 五、高阶偏导数

- 六、多元函数的极值

- 七、条件极值

- 第八章重积分

- 一、重积分的概念及性质

- 二、累次积分

- 三、重积分的计算

- 四、重积分的应用

- 第九章曲线积分与曲面积分

- 一、平面向量场

- 二、曲线的向量表示

- 三、第一型曲线积分

- 四、第二型曲线积分

- 五、格林公式及其应用

- 六、空间向量场

- 七、曲面的向量表示

- 八、第一型曲面积分

- 九、第二型曲面积分

- 十、斯托克斯公式及其应用

- 第十章常微分方程

- 一、基本概念与初值问题

- 二、可分离变量的方程

- 三、一阶线性微分方程

- 四、可降阶的高阶微分方程

- 五、常系数齐次线性微分方程

- 六、常系数非齐次线性微分方程

- 七、欧拉方程

- 八、常系数线性齐次方程组

- 第十一章傅里叶级数

- 一、周期函数与傅里叶级数

- 二、傅里叶级数的收敛性

- 三、奇偶性和卷积公式

- 四、复合周期函数的傅里叶级数

- 五、傅里叶级数的应用

查看详情

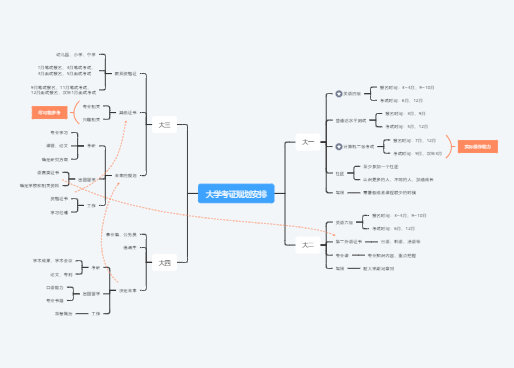
模板简介

同济大学出版社的高等数学的思维导图，如有不对，欢迎指正！

猜你喜欢

相关文章

八下历史思维导图-第五单元内容整理2022-07-20 七下历史思维导图-唐朝的兴盛思维导图2022-07-19 小数的初步认识思维导图-三年级下册数学脑图整理2022-07-18 八年级生物上册第一章思维导图：动物的主要类群2021-08-29 八年级生物上册第六单元思维导图：生物的多样性及其保护2021-08-28 八年级生物上册第五单元思维导图：生物圈中的其他生物2021-08-28 小学六年级上册数学思维导图：百分数2021-08-26 小学六年级上册数学思维导图：圆2021-08-25 小学六年级上册数学思维导图：比2021-08-24 小学六年级上册数学思维导图：分数乘法2021-08-23 小学六年级上册数学思维导图-全书2021-08-22 九年级上册政治思维导图：中国梦-初三知识点脑图整理2021-08-21 七年级上册地理思维导图：地球和地球仪2021-08-20 高中历史必修一思维导图：现代中国的政治建设与祖国统一2021-08-19 高中历史必修三思维导图：中国近代前期思想变化2021-08-18 高中历史必修二思维导图：中国近代前期政治2021-08-17

您的想法与建议，对知犀思维导图的优化改进非常有用！欢迎反馈！