负数:比0小的数
正数:比0大的数
0既不是正数也不是负数
注意:a表示任意数时,不一定是负数,当a<0则-a为正数
负数可以表示该正数相反意义的量
举例:零上8℃表示+8℃;零下8℃表示为-8℃
表示没有
正负数的分界线
乘积是1的两个数互为倒数,其中一个数叫做另一个数的倒数,用式子表示为a•1/a(a≠0),
就是说a和1/a互为倒数
①0没有倒数
②求假分数或真分数的倒数,只要把这个分数的分子、分母点颠倒位置即可;
求带分数的倒数时,先把带分数化为假分数,再把分子、分母颠倒位置
③正数的倒数是正数,负数的倒数是负数(求一个数的倒数,不改变这个数的性质)
④倒数等于它本身的数是1或-1,不包括0
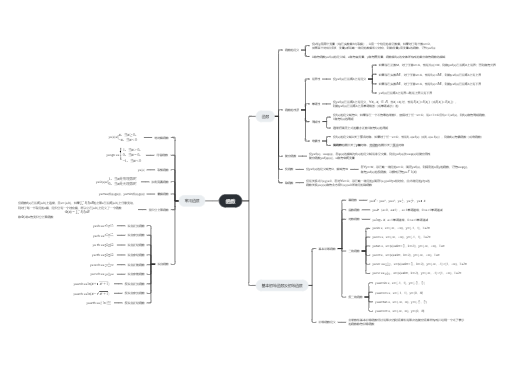
正整数、0、负整数统称为正数(0和正整数统称为自然数)
正分数和负分数统称为分数
正整数,0,负整数,正分数,负分数都可以写成分数的形式,这样的数称为有理数
①π是无限不循环小数,不能写成分数形式,不是有理数
②有理小数和无限循环小数都可化成分数,都是有理数
正整数
0
负整数
正分数
负分数
无限不循环小数
正整数
正分数
0
负整数
负分数
同号两数相加,取相同的符号,并把绝对值相加
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值
互为相反数的两数相加,和为零
一个数与零相加,仍得这个数
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
①互为相反数的两个数先相加——“相反数结合法"
②符号相同的两个数先相加——"同号结合法"
③分母相同的数先相加——"同分母结合法"
④几个数相加得到整数,先相加——"凑整法"
⑤整数与整数、小数与小数相加——“同形结合法"
b>0,a+b>a
b=0,a+b=a
a-b=a+(-b)
两数相乘,同号得正,异号得负,并把绝对值相乘
任何数同0相乘,都得0
几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,
积是负数
几个数相乘,如果其中有因数为0,则积等于0
乘法交换律:一般的,有理数乘法中,两个数相乘,交换因数的位置,积相等。即ab=ba
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。即(ab)c=a(bc)
乘法分配律:一般的,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,在把积相加。
即a(b+c)=ab+ac
除以一个不等0的数,等于乘以这个数的倒数
两数相除,同号得正,异号得负,并把绝对值相除。0除以任何一个不等于0的数,都得0
乘除混合运算往往先将除法化成乘法,然后确定积的符号,最后求出结果
有理数的加减乘除混合运算,如无括号指出先做什么运算,则按照“先乘除,后加减”的顺序进行
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂
负数的奇次幂是负数,偶次幂的正数
正数的任何次幂都是正数
0的任何正整数次幂都是0
1的任何次幂都是1,-1的偶次幂是1,奇次幂是-1
①先乘方,再乘除,最后加减
②同级运算,从左到右进行
③如有括号,先做括号内的运算,按小括号,中括号,大括号依次进行
有限小数、无限循环小数