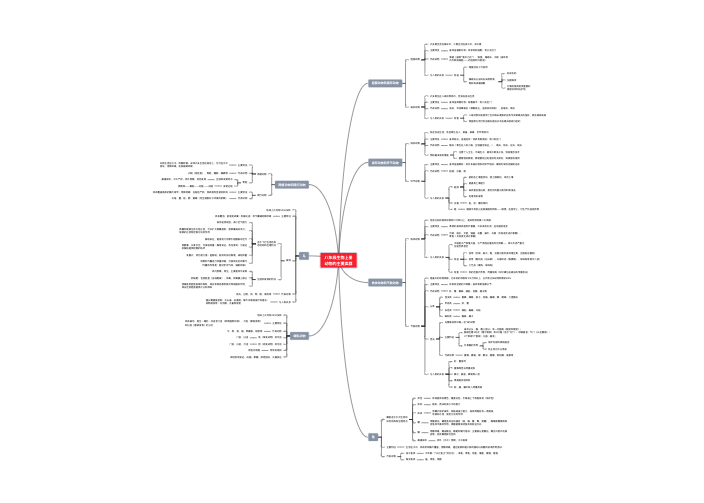
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴
折叠后重合的点是对应点,叫做对称点
正n边形有n条对称轴
如果两个图形关于某条直线对称,
那么对称轴是任何一对对应点所连连线段的垂直平分线
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线
线段垂直平分线上的点与这条线段两个端点的距离相等
与线段两个端点距离相等的点在这条线段的垂直平分线上
轴对称得到图形与原图形的形状、大小完全相同
新图形上的每一点,都是原图形上的某一点关于对称轴直线的对称点
连接任意一对对应点所连线段被对称轴垂直平分
几何图形都可以看作由点组成,对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形
关于x轴对称:横不变,纵相反(x轴x不变)
关于y轴对称:横相反,纵不变(y轴y不变)
关于原点对称:横纵坐标都互为相反数
有两边相等的三角形是等腰三角形
等边对等角:
等腰三角形的两个底角相等
三线合一:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
等角对等边
如果一个三角形有两个角相等,那么这两个角所对的边也相等
三条边都相等的三角形叫做等边三角形
等边三角形的三个内角都相等,并且每一个角都等于60°
三个角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
轴对称图形,每条边都有三线合一
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
构造全等三角形(中线倍长,一线三等角,垂直)
构造等腰三角形(三线中一线,平行线,截长补短,截边等构造60°)
通过利用轴对称、平移等变化把已知问题转化为容易解决的问题
从而作出最短路径的选择(异侧共线和最小,同侧共线差最大)
过一点做已知直线的垂线
作已知线段的垂直平分线
作已知线段的中点
作一种图形的轴对称图形
作等腰三角形
作最短路径